Converting to & from `tf`

Functional data have often been stored in matrices or data frames. Although these structures have sufficed for some purposes, they are cumbersome or impossible to use with modern tools for data wrangling.

In this vignette, we illustrate how to convert data from common structures to tf objects. Throughout, functional data vectors are stored as columns in a data frame to facilitate subsequent wrangling and analysis.

Conversion from matrices

One of the most common structures for storing functional data has been a matrix. Especially when subjects are observed over the same (regular or irregular) grid, it is natural to observations on a subject in rows (or columns) of a matrix. Matrices, however, are difficult to wrangle along with data in a data frame, leading to confusing and easy-to-break subsetting across several objects.

In the following examples, we’ll use tfd to get a tf vector from matrices. The tfd function expects data to be organized so that each row is the functional observation for a single subject. It’s possible to focus only on the resulting tf vector, but in keeping with the broader goals of tidyfun we’ll add these as columns to a data frame.

The DTI data in the refund package has been a popular example in functional data analysis. In the code below, we create a data frame (or tibble) containing scalar covariates, and then add columns for the cca and rcst track profiles. This code was used to create the tidyfun::dti_df dataset included in the package.

dti_df <- tibble(
  id = refund::DTI$ID,
  visit = refund::DTI$visit,
  sex = refund::DTI$sex,
  case = factor(ifelse(refund::DTI$case, "MS", "control"))
)

dti_df$cca <- tfd(refund::DTI$cca, arg = seq(0, 1, length.out = 93))
dti_df$rcst <- tfd(refund::DTI$rcst, arg = seq(0, 1, length.out = 55))

In tfd, the first argument is a matrix; arg defines the grid over which functions are observed. The output of tfd is a vector, which we include in the dti_df data frame.

dti_df
## # A tibble: 382 × 6
##       id visit sex    case                                                  cca
##    <dbl> <int> <fct>  <fct>                                          <tfd_irrg>
##  1  1001     1 female control  [1]: (0.000,0.49);(0.011,0.52);(0.022,0.54); ...
##  2  1002     1 female control  [2]: (0.000,0.47);(0.011,0.49);(0.022,0.50); ...
##  3  1003     1 male   control  [3]: (0.000,0.50);(0.011,0.51);(0.022,0.54); ...
##  4  1004     1 male   control  [4]: (0.000,0.40);(0.011,0.42);(0.022,0.44); ...
##  5  1005     1 male   control  [5]: (0.000,0.40);(0.011,0.41);(0.022,0.40); ...
##  6  1006     1 male   control  [6]: (0.000,0.45);(0.011,0.45);(0.022,0.46); ...
##  7  1007     1 male   control  [7]: (0.000,0.55);(0.011,0.56);(0.022,0.56); ...
##  8  1008     1 male   control  [8]: (0.000,0.45);(0.011,0.48);(0.022,0.50); ...
##  9  1009     1 male   control  [9]: (0.000,0.50);(0.011,0.51);(0.022,0.52); ...
## 10  1010     1 male   control [10]: (0.000,0.46);(0.011,0.47);(0.022,0.48); ...
## # ℹ 372 more rows
## # ℹ 1 more variable: rcst <tfd_irrg>

Finally, we’ll make a quick spaghetti plot to illustrate that the complete functional data is included in each tf column.

dti_df |>
  ggplot() +
  geom_spaghetti(aes(y = cca, col = case, alpha = 0.2 + 0.4 * (case == "control"))) +
  facet_wrap(~sex) +
  scale_alpha(guide = "none", range = c(0.2, 0.4))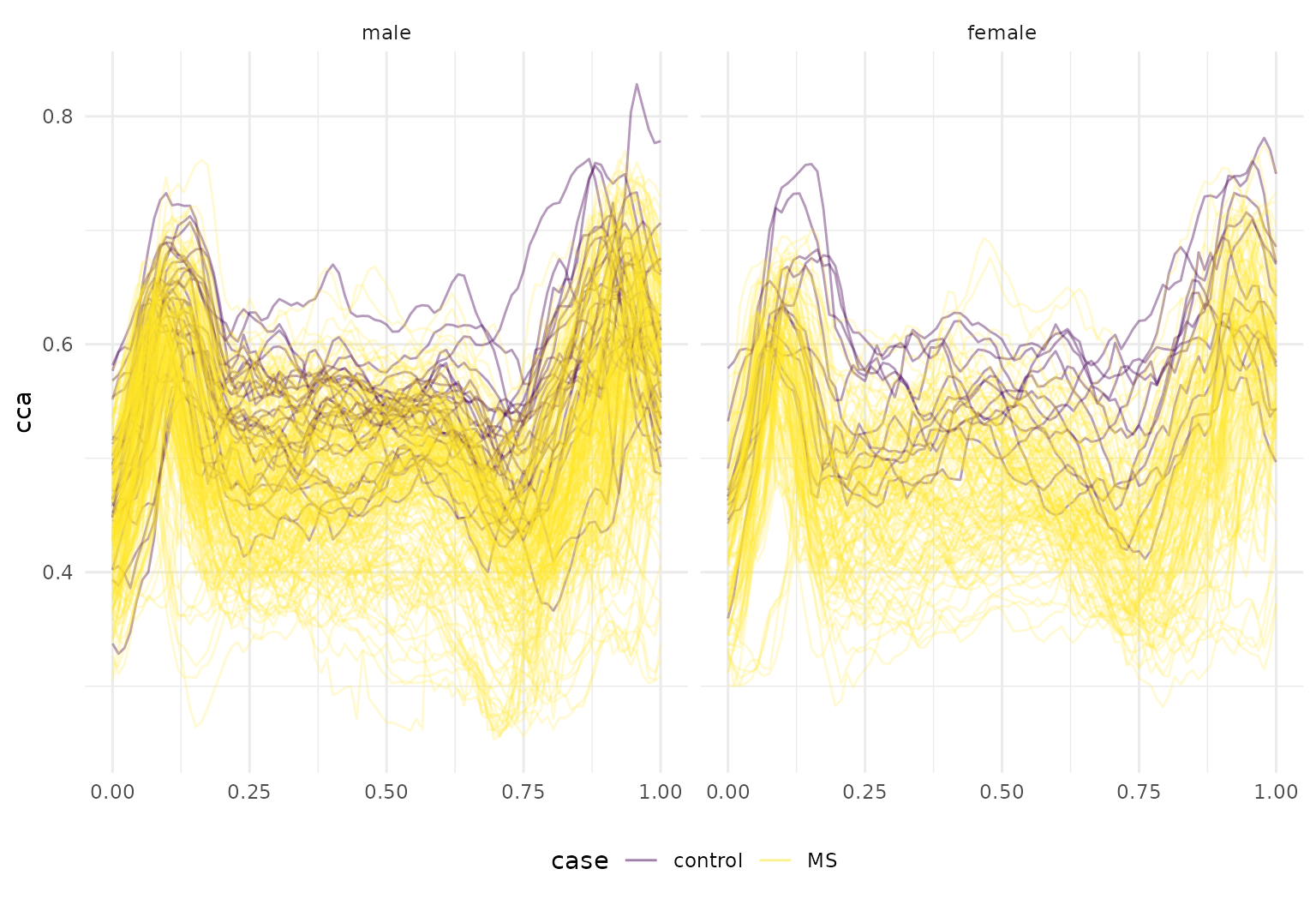

We’ll repeat the same basic process using a second, and probably even-more-perennial, functional data example: the Canadian weather data in the fda package. Here, functional data are stored in a three-dimensional array, with dimensions corresponding to day, station, and outcome (temperature, precipitation, and log10 precipitation).

In the following, we first create a tibble with scalar covariates, then use tfd to create functional data vectors, and finally include the resulting vectors in the dataframe. In this case, our args are days of the year, and we use tf_smooth to smooth the precipitation outcome. Because the original data matrices record the different observations in the columns instead of the rows, we have to use their transpose in the call to tfd:

canada <- tibble(
  place = fda::CanadianWeather$place,
  region = fda::CanadianWeather$region,
  lat = fda::CanadianWeather$coordinates[, 1],
  lon = -fda::CanadianWeather$coordinates[, 2]
) |>
  mutate(
    temp = t(fda::CanadianWeather$dailyAv[, , 1]) |>
      tfd(arg = 1:365),
    precipl10 = t(fda::CanadianWeather$dailyAv[, , 3]) |>
      tfd(arg = 1:365) |>
      tf_smooth()
  )
## using f = 0.15 as smoother span for lowess

The resulting data frame is shown below.

canada
## # A tibble: 35 × 6
##    place       region     lat   lon                               temp
##    <chr>       <chr>    <dbl> <dbl>                          <tfd_reg>
##  1 St. Johns   Atlantic  47.3 -52.4  [1]: (1, -4);(2, -3);(3, -3); ...
##  2 Halifax     Atlantic  44.4 -63.4  [2]: (1, -4);(2, -4);(3, -5); ...
##  3 Sydney      Atlantic  46.1 -60.1  [3]: (1, -4);(2, -4);(3, -5); ...
##  4 Yarmouth    Atlantic  43.5 -66.1  [4]: (1, -1);(2, -2);(3, -2); ...
##  5 Charlottvl  Atlantic  42.5 -80.2  [5]: (1, -6);(2, -6);(3, -7); ...
##  6 Fredericton Atlantic  45.6 -66.4  [6]: (1, -8);(2, -8);(3, -9); ...
##  7 Scheffervll Atlantic  54.5 -64.5  [7]: (1,-22);(2,-23);(3,-23); ...
##  8 Arvida      Atlantic  48.3 -71.1  [8]: (1,-14);(2,-14);(3,-15); ...
##  9 Bagottville Atlantic  48.2 -70.5  [9]: (1,-15);(2,-15);(3,-16); ...
## 10 Quebec      Atlantic  46.5 -71.1 [10]: (1,-11);(2,-11);(3,-12); ...
## # ℹ 25 more rows
## # ℹ 1 more variable: precipl10 <tfd_reg>

A plot containing both functional observations is shown below.

temp_panel <- canada |>
  ggplot(aes(y = temp, color = region)) +
  geom_spaghetti()

precip_panel <- canada |>
  ggplot(aes(y = precipl10, color = region)) +
  geom_spaghetti()

gridExtra::grid.arrange(temp_panel, precip_panel, nrow = 1)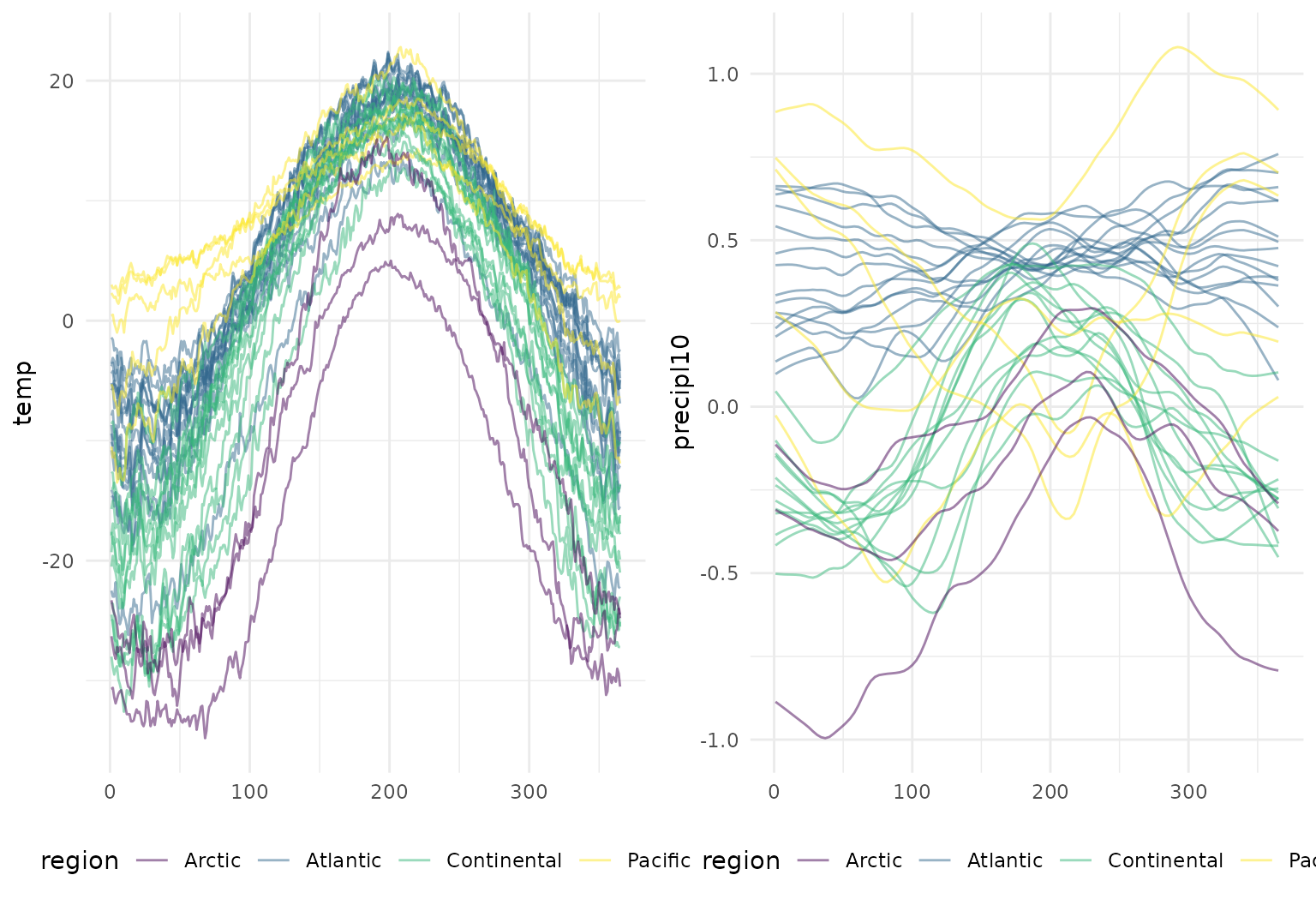

Conversion to `tf` from a data frame

… in “long” format

“Long” format data frames containing functional data include columns containing a subject identifier, the functional argument, and the value each subject’s function takes at each argument. There are also often (but not always) non-functional covariates that are repeated within a subject. For data in this form, we use tf_nest to produce a data frame containing a single row for each subject.

A first example is the pig weight data from the SemiPar package, which is a nice example from longitudinal data analysis. This includes columns for id.num, num.weeks, and weight – which correspond to the subject, argument, and value.

data("pig.weights", package = "SemiPar")

pig.weights <- as_tibble(pig.weights)

pig.weights
## # A tibble: 432 × 3
##    id.num num.weeks weight
##     <int>     <int>  <dbl>
##  1      1         1   24  
##  2      1         2   32  
##  3      1         3   39  
##  4      1         4   42.5
##  5      1         5   48  
##  6      1         6   54.5
##  7      1         7   61  
##  8      1         8   65  
##  9      1         9   72  
## 10      2         1   22.5
## # ℹ 422 more rows

We create pig_df by nesting weight within subject. The result is a data frame containing a single row for each pig, and columns for id.num and the weight function.

pig_df <- pig.weights |>
  tf_nest(weight, .id = id.num, .arg = num.weeks)

pig_df
## # A tibble: 48 × 2
##    id.num                          weight
##     <int>                       <tfd_reg>
##  1      1  [1]: (1,24);(2,32);(3,39); ...
##  2      2  [2]: (1,22);(2,30);(3,40); ...
##  3      3  [3]: (1,22);(2,28);(3,36); ...
##  4      4  [4]: (1,24);(2,32);(3,40); ...
##  5      5  [5]: (1,24);(2,32);(3,37); ...
##  6      6  [6]: (1,23);(2,30);(3,36); ...
##  7      7  [7]: (1,22);(2,28);(3,36); ...
##  8      8  [8]: (1,24);(2,30);(3,38); ...
##  9      9  [9]: (1,20);(2,28);(3,33); ...
## 10     10 [10]: (1,26);(2,32);(3,40); ...
## # ℹ 38 more rows

We’ll make a quick plot to show the result.

pig_df |>
  ggplot(aes(y = weight)) +
  geom_spaghetti()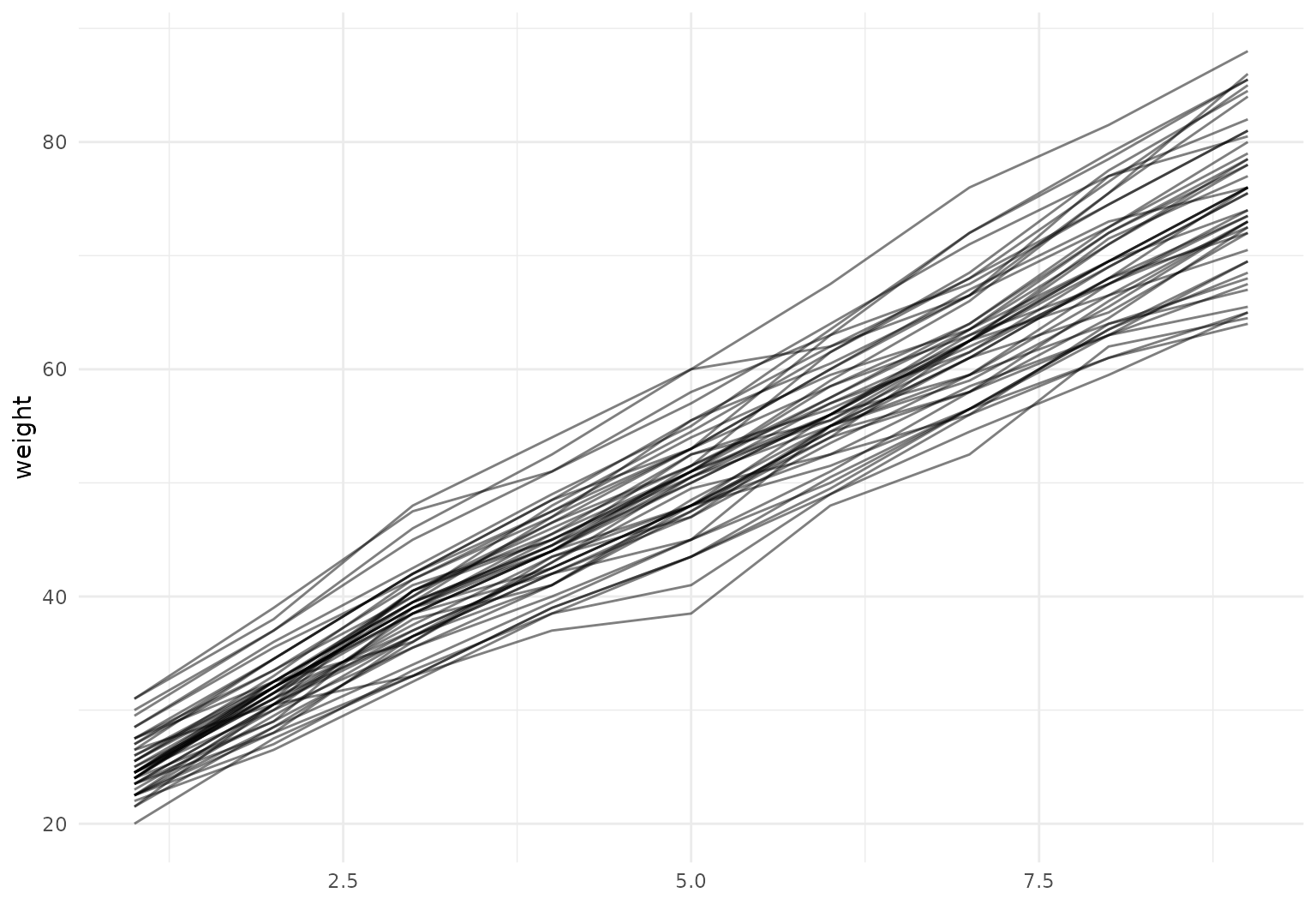

A second example uses the ALA::fev1 dataset. ALA is not available on CRAN but can be installed using the line below.

install.packages("ALA", repos = "http://R-Forge.R-project.org")

In this dataset, both height and logFEV1 are observed at multiple ages for each child; that is, there are two functions observed simultaneously, over a shared argument. We can use tf_nest to create a dataframe with a single row for each subject, which includes both non-functional covariates (like age and height at baseline), and functional observations logFEV1 and height.

ALA::fev1 |> glimpse()
## Rows: 1,994
## Columns: 6
## $ id      <fct> 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, …
## $ age     <dbl> 9.3415, 10.3929, 11.4524, 12.4600, 13.4182, 15.4743, 16.3723, 6.5873, 7.6496, 12.7392, 13.7741, 14.6940, 15.…
## $ height  <dbl> 1.20, 1.28, 1.33, 1.42, 1.48, 1.50, 1.52, 1.13, 1.19, 1.49, 1.53, 1.55, 1.56, 1.57, 1.57, 1.18, 1.23, 1.30, …
## $ age0    <dbl> 9.3415, 9.3415, 9.3415, 9.3415, 9.3415, 9.3415, 9.3415, 6.5873, 6.5873, 6.5873, 6.5873, 6.5873, 6.5873, 6.58…
## $ height0 <dbl> 1.20, 1.20, 1.20, 1.20, 1.20, 1.20, 1.20, 1.13, 1.13, 1.13, 1.13, 1.13, 1.13, 1.13, 1.13, 1.18, 1.18, 1.18, …
## $ logFEV1 <dbl> 0.21511, 0.37156, 0.48858, 0.75142, 0.83291, 0.89200, 0.87129, 0.30748, 0.35066, 0.75612, 0.86710, 1.04732, …
ALA::fev1 |>
  group_by(id) |>
  mutate(n_obs = n()) |>
  filter(n_obs > 1) |>
  tf_nest(logFEV1, height, .arg = age) |>
  glimpse()
## Rows: 252
## Columns: 6
## $ id      <fct> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 15, 16, 18, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 3…
## $ age0    <dbl> 9.3415, 6.5873, 6.9131, 6.7598, 6.5024, 6.8994, 6.4339, 7.1869, 6.8966, 7.7892, 7.6140, 7.5483, 7.8412, 6.50…
## $ height0 <dbl> 1.20, 1.13, 1.18, 1.15, 1.11, 1.24, 1.18, 1.27, 1.17, 1.13, 1.32, 1.25, 1.25, 1.20, 1.19, 1.24, 1.21, 1.23, …
## $ n_obs   <int> 7, 8, 9, 10, 7, 11, 7, 9, 9, 10, 6, 3, 5, 11, 12, 10, 9, 8, 12, 2, 2, 11, 11, 7, 9, 11, 11, 4, 2, 12, 3, 9, …
## $ logFEV1 <tfd_irrg> [<9.3415, 10.3929, 11.4524, 12.4600, 13.4182, 15.4743, 16.3723>, <0.21511, 0.37156, 0.48858, 0.75142, 0…
## $ height  <tfd_irrg> [<9.3415, 10.3929, 11.4524, 12.4600, 13.4182, 15.4743, 16.3723>, <1.20, 1.28, 1.33, 1.42, 1.48, 1.50, 1…

… in “wide” format

In some cases functional data are stored in “wide” format, meaning that there are separate columns for each argument, and values are stored in these columns. In this case, tf_gather can be use to collapse across columns to produce a function for each subject.

The example below again uses the refund::DTI dataset. We use tf_gather to transfer the cca observations from a matrix column (with NAs) into a column of irregularly observed functions (tfd_irreg).

dti_df <- refund::DTI |>
  janitor::clean_names() |>
  select(-starts_with("rcst")) |>
  glimpse()
## Rows: 382
## Columns: 8
## $ id         <dbl> 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009, 1010,…
## $ visit      <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ visit_time <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
## $ nscans     <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ case       <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
## $ sex        <fct> female, female, male, male, male, male, male, male, male, m…
## $ pasat      <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
## $ cca        <dbl[,93]> <matrix[26 x 93]>

dti_df |>
  tf_gather(starts_with("cca")) |>
  glimpse()
## creating new tfd-column <cca>
## Rows: 382
## Columns: 8
## $ id         <dbl> 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009, 1010,…
## $ visit      <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ visit_time <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
## $ nscans     <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ case       <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
## $ sex        <fct> female, female, male, male, male, male, male, male, male, m…
## $ pasat      <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
## $ cca        <tfd_irrg> [<1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1…

Other formats

fda and fd coming soon …

Reversing the conversion

tidyfun includes a wide range of tools for exploratory analysis and visualization, but many analysis approaches require data to be stored in more traditional formats. Several functions are available to aid in this conversion.

Conversion from `tf` to data frames

The functions tf_unnest and tf_spread reverse the operations in tf_nest and tf_gather, respectively – that is, they take a data frame with a functional observation and produce long or wide data frames. We’ll illustrate these with the pig_df data set.

First, to produce a long-format data frame, one can use tf_unnest:

pig_df |>
  tf_unnest(cols = weight) |>
  glimpse()
## Rows: 432
## Columns: 3
## $ id.num       <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, …
## $ weight_arg   <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, …
## $ weight_value <dbl> 24.0, 32.0, 39.0, 42.5, 48.0, 54.5, 61.0, 65.0, 72.0, 22.…

To produce a wide-format data frame, one can use tf_spread:

pig_df |>
  tf_spread() |>
  glimpse()
## Rows: 48
## Columns: 10
## $ id.num   <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18…
## $ weight_1 <dbl> 24.0, 22.5, 22.5, 24.0, 24.5, 23.0, 22.5, 23.5, 20.0, 25.5, 2…
## $ weight_2 <dbl> 32.0, 30.5, 28.0, 31.5, 31.5, 30.0, 28.5, 30.5, 27.5, 32.5, 3…
## $ weight_3 <dbl> 39.0, 40.5, 36.5, 39.5, 37.0, 35.5, 36.0, 38.0, 33.0, 39.5, 4…
## $ weight_4 <dbl> 42.5, 45.0, 41.0, 44.5, 42.5, 41.0, 43.5, 41.0, 39.0, 47.0, 4…
## $ weight_5 <dbl> 48.0, 51.0, 47.5, 51.0, 48.0, 48.0, 47.0, 48.5, 43.5, 53.0, 5…
## $ weight_6 <dbl> 54.5, 58.5, 55.0, 56.0, 54.0, 51.5, 53.5, 55.0, 49.0, 58.5, 5…
## $ weight_7 <dbl> 61.0, 64.0, 61.0, 59.5, 58.0, 56.5, 59.5, 59.5, 54.5, 63.0, 6…
## $ weight_8 <dbl> 65.0, 72.0, 68.0, 64.0, 63.0, 63.5, 67.5, 66.5, 59.5, 69.5, 6…
## $ weight_9 <dbl> 72.0, 78.0, 76.0, 67.0, 65.5, 69.5, 73.5, 73.0, 65.0, 76.0, 7…

Converting back to a matrix or data frame

To convert tf vector to a matrix with each row containing the function evaluations for one function, use as.matrix:

weight_vec <- pig_df$weight

weight_matrix <- weight_vec |> as.matrix()

head(weight_matrix)
##      1    2    3    4    5    6    7    8    9
## 1 24.0 32.0 39.0 42.5 48.0 54.5 61.0 65.0 72.0
## 2 22.5 30.5 40.5 45.0 51.0 58.5 64.0 72.0 78.0
## 3 22.5 28.0 36.5 41.0 47.5 55.0 61.0 68.0 76.0
## 4 24.0 31.5 39.5 44.5 51.0 56.0 59.5 64.0 67.0
## 5 24.5 31.5 37.0 42.5 48.0 54.0 58.0 63.0 65.5
## 6 23.0 30.0 35.5 41.0 48.0 51.5 56.5 63.5 69.5

# argument values of input data saved in `arg`-attribute:
attr(weight_matrix, "arg")
## [1] 1 2 3 4 5 6 7 8 9

To convert a tf vector to a standalone data frame with "id","arg","value"-columns, use as.data.frame() with unnest = TRUE:

weight_vec
## tfd[48] on (1,9) based on 9 evaluations each
## interpolation by tf_approx_linear 
## 1: (1,24);(2,32);(3,39); ...
## 2: (1,22);(2,30);(3,40); ...
## 3: (1,22);(2,28);(3,36); ...
## 4: (1,24);(2,32);(3,40); ...
## 5: (1,24);(2,32);(3,37); ...
##     [....]   (43 not shown)

weight_vec |>
  as.data.frame(unnest = TRUE) |>
  head()
##     id arg value
## 1.1  1   1  24.0
## 1.2  1   2  32.0
## 1.3  1   3  39.0
## 1.4  1   4  42.5
## 1.5  1   5  48.0
## 1.6  1   6  54.5

Jeff Goldsmith, Fabian Scheipl

2024-02-23

Conversion from matrices

Conversion to `tf` from a data frame

… in “long” format

… in “wide” format

Other formats

Reversing the conversion

Conversion from `tf` to data frames

Converting back to a matrix or data frame

Converting to & from `tf`

Jeff Goldsmith, Fabian Scheipl

2024-02-23

Conversion from matrices

Conversion to tf from a data frame

… in “long” format

… in “wide” format

Other formats

Reversing the conversion

Conversion from tf to data frames

Converting back to a matrix or data frame

Conversion to `tf` from a data frame

Conversion from `tf` to data frames