Functional data in FPC-basis representation

These functions perform a (functional) principal component analysis (FPCA) of the input data and return an tfb_fpc tf-object that uses the empirical eigenfunctions as basis functions for representing the data. The default ("method = fpc_wsvd") uses a (truncated) weighted SVD for complete data on a common grid and a nuclear-norm regularized (truncated) weighted SVD for partially missing data on a common grid, see fpc_wsvd(). The latter is likely to break down for high PVE and/or high amounts of missingness.

Usage

tfb_fpc(data, ...)

# S3 method for data.frame
tfb_fpc(
  data,
  id = 1,
  arg = 2,
  value = 3,
  domain = NULL,
  method = fpc_wsvd,
  ...
)

# S3 method for matrix
tfb_fpc(data, arg = NULL, domain = NULL, method = fpc_wsvd, ...)

# S3 method for numeric
tfb_fpc(data, arg = NULL, domain = NULL, method = fpc_wsvd, ...)

# S3 method for tf
tfb_fpc(data, arg = NULL, method = fpc_wsvd, ...)

# S3 method for default
tfb_fpc(data, arg = NULL, domain = NULL, method = fpc_wsvd, ...)

Arguments

data: a matrix, data.frame or list of suitable shape, or another tf-object containing functional data.
...: arguments to the method which computes the (regularized/smoothed) FPCA - see e.g. fpc_wsvd(). Unless set by the user, uses proportion of variance explained pve = 0.995 to determine the truncation levels.
id: The name or number of the column defining which data belong to which function.
arg: numeric, or list of numerics. The evaluation grid. For the data.frame-method: the name/number of the column defining the evaluation grid. The matrix method will try to guess suitable arg-values from the column names of data if arg is not supplied. Other methods fall back on integer sequences (1:<length of data>) as the default if not provided.
value: The name or number of the column containing the function evaluations.
domain: range of the arg.
method: the function to use that computes eigenfunctions and scores. Defaults to fpc_wsvd(), which is quick and easy but returns completely unsmoothed eigenfunctions unlikely to be suited for noisy data. See Details.

Value

an object of class tfb_fpc, inheriting from tfb. The basis used by tfb_fpc is a tfd-vector containing the estimated mean and eigenfunctions.

Details

For the FPC basis, any factorization method that accepts a data.frame with columns id, arg, value containing the functional data and returns a list with eigenfunctions and FPC scores structured like the return object of fpc_wsvd() can be used for the `method`` argument, see example below. Note that the mean function, with a fixed "score" of 1 for all functions, is used as the first basis function for all FPC bases.

Methods (by class)

tfb_fpc(default): convert tfb: default method, returning prototype when data is NULL

Examples

set.seed(13121)
x <- tf_rgp(25, nugget = .02)
x_pc <- tfb_fpc(x, pve = .9)
x_pc
#> tfb[25] on (0,1) in basis representation:
#>  using  4 FPCs 
#> 1: (0.00,-0.138);(0.02,-0.067);(0.04,-0.046); ...
#> 2: (0.00,  0.12);(0.02,  0.20);(0.04,  0.18); ...
#> 3: (0.00, -0.94);(0.02, -0.91);(0.04, -1.02); ...
#> 4: (0.00, -0.40);(0.02, -0.21);(0.04, -0.19); ...
#> 5: (0.00,  -1.5);(0.02,  -1.5);(0.04,  -1.5); ...
#>     [....]   (20 not shown)
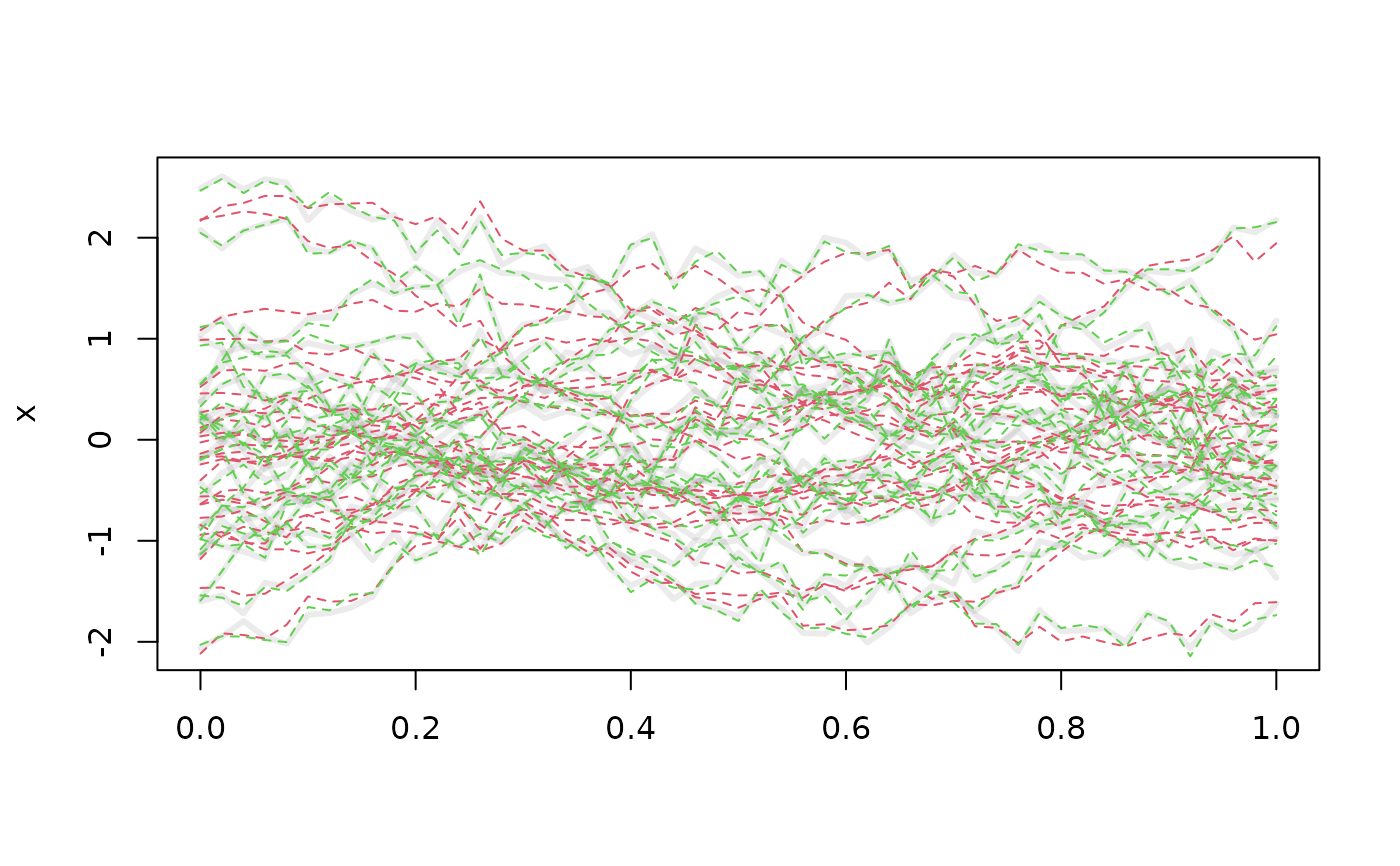
plot(x, lwd = 3)
lines(x_pc, col = 2, lty = 2)
x_pc_full <- tfb_fpc(x, pve = .995)
x_pc_full
#> tfb[25] on (0,1) in basis representation:
#>  using  15 FPCs 
#> 1: (0.00, 0.172);(0.02,-0.019);(0.04, 0.238); ...
#> 2: (0.00,  0.20);(0.02,  0.37);(0.04,  0.29); ...
#> 3: (0.00, -0.98);(0.02, -1.05);(0.04, -1.03); ...
#> 4: (0.00, -0.99);(0.02, -0.65);(0.04, -0.47); ...
#> 5: (0.00,  -1.5);(0.02,  -1.6);(0.04,  -1.6); ...
#>     [....]   (20 not shown)
lines(x_pc_full, col = 3, lty = 2)

# partially missing data on common grid:
x_mis <- x |> tf_sparsify(dropout = .05)
x_pc_mis <- tfb_fpc(x_mis, pve = .9)
#> Using softImpute SVD on 5.3% missing data
x_pc_mis
#> tfb[25] on (0,1) in basis representation:
#>  using  4 FPCs 
#> 1: (0.00,-0.207);(0.02,-0.084);(0.04,-0.046); ...
#> 2: (0.00, 0.055);(0.02, 0.167);(0.04, 0.197); ...
#> 3: (0.00, -0.85);(0.02, -0.78);(0.04, -0.78); ...
#> 4: (0.00, -0.34);(0.02, -0.20);(0.04, -0.15); ...
#> 5: (0.00,  -1.5);(0.02,  -1.4);(0.04,  -1.4); ...
#>     [....]   (20 not shown)
plot(x_mis, lwd = 3)
lines(x_pc_mis, col = 4, lty = 2)

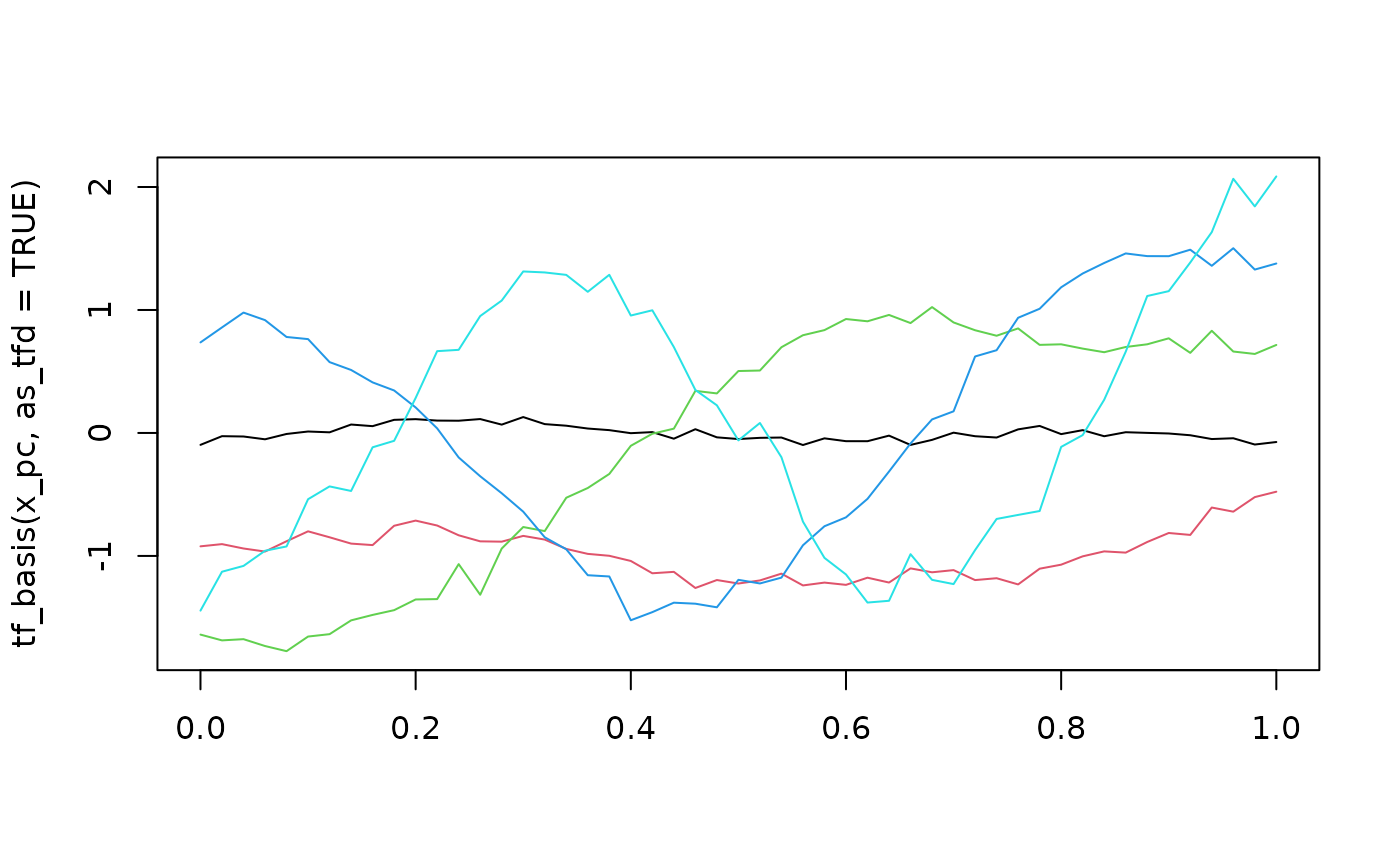
# extract FPC basis --
# first "eigenvector" in black is (always) the mean function
x_pc |> tf_basis(as_tfd = TRUE) |> plot(col = 1:5)

# \donttest{
# Apply FPCA for sparse, irregular data using refund::fpca.sc:
set.seed(99290)
# create small, sparse, irregular data:
x_irreg <- x[1:8] |>
  tf_jiggle() |> tf_sparsify(dropout = 0.3)
plot(x_irreg)
x_df <- x_irreg |>
  as.data.frame(unnest = TRUE)
# wrap refund::fpca_sc for use as FPCA method in tfb_fpc --
# 1. define scoring function (simple weighted LS fit)
fpca_scores <- function(data_matrix, efunctions, mean, weights) {
  w_mat <- matrix(weights, ncol = length(weights), nrow = nrow(data_matrix),
                  byrow = TRUE)
  w_mat[is.na(data_matrix)] <- 0
  data_matrix[is.na(data_matrix)] <- 0
  data_wc <- t((t(data_matrix) - mean) * sqrt(t(w_mat)))
  t(qr.coef(qr(efunctions), t(data_wc) / sqrt(weights)))
}
# 2. define wrapper for fpca_sc:
fpca_sc_wrapper <- function(data, arg, pve = 0.995, ...) {
  data_mat <- tfd(data) |> as.matrix(interpolate = TRUE)
  fpca <- refund::fpca.sc(
    Y = data_mat, argvals = attr(data_mat, "arg"), pve = pve, ...
  )
  c(fpca[c("mu", "efunctions", "scores", "npc")],
    scoring_function = fpca_scores)
}
x_pc <- tfb_fpc(x_df, method = fpca_sc_wrapper)
lines(x_pc, col = 2, lty = 2)

# }